ZIB PaperWeb
On the Complexity of Vertex-Disjoint Length-Restricted Path
Problems
SC 98-20 Andreas Bley: On the Complexity of Vertex-Disjoint Length-Restricted Path
Problems
Abstract: Let G=(V,E) be a simple graph and s and t be two distinct
vertices of
G. A path in G is called 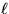 -bounded for some
-bounded for some 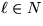 , if
it does not contain more than
, if
it does not contain more than 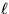 edges. We study the computational
complexity of approximating the optimum value for two optimization problems
of finding sets of vertex-disjoint
edges. We study the computational
complexity of approximating the optimum value for two optimization problems
of finding sets of vertex-disjoint 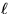 -bounded s,t-paths in G.
-bounded s,t-paths in G.
First, we show that computing the maximum number of vertex-disjoint
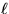 -bounded s,t-paths is
-bounded s,t-paths is 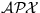 -complete for any
fixed length bound
-complete for any
fixed length bound 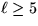 .
.
Second, for a given number 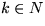 ,
, 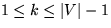 , and
non-negative weights on the edges of G, the problem of finding k
vertex-disjoint
, and
non-negative weights on the edges of G, the problem of finding k
vertex-disjoint 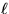 -bounded s,t-paths with minimal total weight is
proven to be
-bounded s,t-paths with minimal total weight is
proven to be 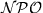 -complete for any length bound
-complete for any length bound 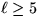 .Furthermore, we show that, even if G is complete, it is
.Furthermore, we show that, even if G is complete, it is
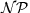 -complete to approximate the optimal solution value of this
problem within a factor of
-complete to approximate the optimal solution value of this
problem within a factor of 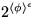 for any constant
for any constant
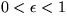 , where
, where 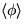 denotes the encoding size of the
given problem instance
denotes the encoding size of the
given problem instance 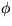 .
.
We prove that these results are tight in the sense that for lengths 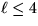 both problems are polynomially solvable, assuming that the weights satisfy
a generalized triangle inequality in the weighted problem.
both problems are polynomially solvable, assuming that the weights satisfy
a generalized triangle inequality in the weighted problem.
All results presented also hold for directed and non-simple graphs. For the
analogous problems where the path length restriction is replaced by the
condition that all paths must have length equal to 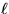 or where
vertex-disjointness is replaced by edge-disjointness we obtain similar
results.
or where
vertex-disjointness is replaced by edge-disjointness we obtain similar
results.
Keywords: disjoint paths,
length bounded paths,
approximation,
reducibility,
completeness
MSC: 68Q25, 90C27, 05C38, 05C40