Abstract: When attempting to compute unsteady, variable density flows at very small or zero Mach number using a standard finite volume compressible flow solver one faces at least the following difficulties: (i) Spatial pressure variations vanish as the Mach number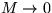
, but they do affect the velocity
field at leading order; (ii) the resulting spatial homogeneity of the leading
order pressure implies an elliptic divergence constraint for the energy flux;
(iii) violation of this constraint would crucially affect the transport of mass,
thereby disabling a code to properly advect even a constant density distribution.
A previous companion paper derived the above observations from a
single time - multiple length scale asymptotic analysis for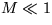 
,applied to the conservation form of the governing equations and assuming
an ideal gas with constant specific heats. The paper then restricted to weakly
compressible one-dimensional flows and introduced a semi-implicit extension of
a compressible flow solver, designed to handle the interaction of long wavelength
acoustics with small scale, large amplitude density fluctuations.
In the present paper we concentrate on the limit of zero Mach number for
multi-dimensional, variable density flows. The construction of numerical
fluxes for all conserved quantities involves: An explicit upwind step (1)
yielding predictions for the nonlinear convective flux components. This
procedure still neglects the influence of pressure gradients on the
convective fluxes during the time step. Suitable corrections are applied in
step (2), which guarantees compliance of the convective fluxes with the
divergence constraint. This step requires the solution of a Poisson-type equation
to obtain the relevant pressure gradients. Step (3), which requires the solution
of a second Poisson-type equation, yields the yet unknown (non-convective) pressure
contribution to the total flux of momentum. The final, cell centered velocity field
exactly satisfies a discrete divergence constraint consistent with the asymptotic
limit. Notice that step (1) can be done by any standard finite volume compressible
flow solver and that the input to steps (2) and (3) involves solely the fluxes from
step (1), but is independent on how these were obtained. Thus, we claim that our
approach allows any such solver to be extended to simulate incompressible flows.
Extensions to the weakly compressible regime 
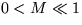, reactive flows and more
complex equations of state will be addressed in follow-up publications.
Keywords: Incompressible variable density flows, conservation laws
MSC: 76D05, 76D30, 76N10, 35L65, 65M99