Abstract: Our focus is on Maxwells equations in the low frequency range; two specific applications we aim at are time-stepping schemes for eddy current computations and the stationary double-curl equation for time-harmonic fields. We assume that the computational domain is discretized by triangles or tetrahedrons; for the finite element approximation we choose N{ed{elecs
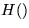-conforming edge elements of the lowest order.
For the
solution of the arising linear equation systems we devise
an
algebraic multigrid preconditioner based on a spatial
component
splitting of the field. Mesh coarsening takes place in an
auxiliary
subspace, which is constructed with the aid of a nodal
vector basis.
Within this subspace coarse grids are created by
exploiting the
matrix graphs. Additionally, we have to cope with the
kernel of the
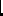-operator, which comprises a considerable part of
the
spectral modes on the grid. Fortunately, the kernel modes
are
accessible via a discrete Helmholtz decomposition of the
fields;
they are smoothed by additional algebraic multigrid
cycles.
Numerical experiments are included in order to assess the
efficacy
of the proposed algorithms.
Keywords: Algebraic multigrid, mesh coarsening, edge elements, N{ed{elec spaces, Maxwells equations
MSC: 65-XX, 65N55, 65N30, 65F10, 35Q60