ZIB PaperWeb

Fourth-Order q-Difference Equation for the First Associated of the q-Classical Orthogonal Polynomials

SC 98-06 Mama Foupouagnigni, Andre Ronveaux, Wolfram Koepf: Fourth-Order q-Difference Equation for the First Associated of the q-Classical Orthogonal Polynomials (Appeared in: J. Comp. Appl. Math. 101, pp. 231-236 (1999).)

Abstract: We derive the fourth order q-difference equation satisfied by the first associated of the q-classical orthogonal polynomials.
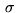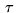The coefficients of this equation are given in terms of the polynomials $\; \sigma\;$ and $\;\tau\;$ which appear in the q-Pearson difference equation 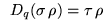$\;\; D_q(\sigma\,\rho)=\tau\,\rho\;$ defining the weight 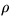$\rho$ of the q-classical orthogonal polynomials inside the q-Hahn tableau.
Keywords: q-Orthogonal polynomials, Fourth order q-difference equation
MSC: 33C25