Carsten Ehrlich:
On the uniqueness of the potential in inverse problems for Schroedinger operators, Zur Eindeutigkeit des Potentials bei inversen Spektralproblemen fuer Schroedingeroperatoren
University: Gerhard-Mercator-Universitaet Duisburg
Department: Fachbereich 11, Mathematik
President of examination commission: Prof. Dr. J. Donig
First Examiner: Prof. Dr. J. Donig
Second Examiner: Prof. Dr. H. Kalf
Abstract: Wir betrachten den Schroedingeroperator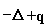 mit gemischten Randbedingungen auf einem beschraenkten Gebiet
mit gemischten Randbedingungen auf einem beschraenkten Gebiet 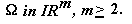 Es sei q ein reellwertiges, bzgl.
Es sei q ein reellwertiges, bzgl. 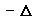 formbeschraenktes Potential aus
formbeschraenktes Potential aus 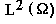 mit relativer Schranke Null. Wir zeigen, dass q eindeutig durch die Eigenwerte, die
Normalenableitungen und die Randwerte der Eigenfunktionen des Schroedingeroperators
bestimmt wird, wobei endlich viele dieser Werte fuer die Bestimmung des Potentials unerheblich sind.
mit relativer Schranke Null. Wir zeigen, dass q eindeutig durch die Eigenwerte, die
Normalenableitungen und die Randwerte der Eigenfunktionen des Schroedingeroperators
bestimmt wird, wobei endlich viele dieser Werte fuer die Bestimmung des Potentials unerheblich sind.
We consider the Schroedinger operator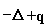 with mixed boundary conditions on a bounded domain
with mixed boundary conditions on a bounded domain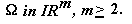 Let
Let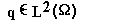 be a real, formbounded potential relative to
be a real, formbounded potential relative to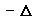 with bound 0. We prove that q is uniquely determined by all but a finite number of the eigenvalues, the normal derivatives and the boundary values of the eigenfunctions of the Schroedinger operator.
with bound 0. We prove that q is uniquely determined by all but a finite number of the eigenvalues, the normal derivatives and the boundary values of the eigenfunctions of the Schroedinger operator.
Keywords: selbstadjungierter Schroedingeroperator, gemischte Randwerte, inverses Spektralproblem, formbeschraenktes Potential, Dirichlet-Neumann-Abbildung, selfadjoint Schroedinger operator, mixed boundary condition, inverse problem, formbounded potential, Dirichlet to Neumann map
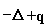 with mixed boundary conditions on a bounded domain
with mixed boundary conditions on a bounded domain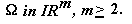 Let
Let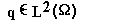 be a real, formbounded potential relative to
be a real, formbounded potential relative to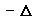 with bound 0. We prove that q is uniquely determined by all but a finite number of the eigenvalues, the normal derivatives and the boundary values of the eigenfunctions of the Schroedinger operator.
with bound 0. We prove that q is uniquely determined by all but a finite number of the eigenvalues, the normal derivatives and the boundary values of the eigenfunctions of the Schroedinger operator.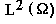 mit relativer Schranke Null. Wir zeigen, dass q eindeutig durch die Eigenwerte, die
Normalenableitungen und die Randwerte der Eigenfunktionen des Schroedingeroperators
bestimmt wird, wobei endlich viele dieser Werte fuer die Bestimmung des Potentials unerheblich sind.
mit relativer Schranke Null. Wir zeigen, dass q eindeutig durch die Eigenwerte, die
Normalenableitungen und die Randwerte der Eigenfunktionen des Schroedingeroperators
bestimmt wird, wobei endlich viele dieser Werte fuer die Bestimmung des Potentials unerheblich sind.