 |
D-Lib Magazine
November/December 2014
Volume 20, Number 11/12
Table of Contents
Extracting Textual Descriptions of Mathematical Expressions in Scientific Papers
Giovanni Yoko Kristianto, The University of Tokyo
giovanni@nii.ac.jp
Goran Topić, National Institute of Informatics, Tokyo, Japan
goran_topic@nii.ac.jp
Akiko Aizawa, The University of Tokyo and National Institute of Informatics, Tokyo, Japan
aizawa@nii.ac.jp
doi:10.1045/november14-kristianto
Printer-friendly Version
Abstract
Mathematical concepts and formulations play a fundamental role in many scientific domains. As such, the use of mathematical expressions represents a promising method of interlinking scientific papers. The purpose of this study is to provide guidelines for annotating and detecting natural language descriptions of mathematical expressions, enabling the semantic enrichment of mathematical information in scientific papers. Under the proposed approach, we first manually annotate descriptions of mathematical expressions and assess the coverage of several types of textual span: fixed context window, apposition, minimal noun phrases, and noun phrases. We then developed a method for automatic description extraction, whereby the problem was formulated as a binary classification by pairing each mathematical expression with its description candidates and classifying the pairs as correct or incorrect. Support vector machines (SVMs) with several different features were developed and evaluated for the classification task. Experimental results showed that an SVM model that uses all noun phrases delivers the best performance, achieving an F1-score of 62.25% against the 41.47% of the baseline (nearest noun) method.
Keywords: Mathematical Expressions, Mathematical Information Access, Description Extraction
1. Introduction
Mathematical concepts and formulations play a fundamental role in many scientific domains. As such, the use of mathematical expressions represents a promising approach to interlinking scientific documents. For example, we can connect a statistical text explaining the Dirichlet distribution with a mathematics paper explaining special functions in calculus and analysis, because both contain the mathematical expression Γ, denoting the gamma function. We can then use this connection to browse several papers and obtain further details about the concept represented by a particular mathematical expression. Such connections can be determined by the structure and textual similarity of the
mathematical expressions.
To detect these implicit connections between mathematical expressions, we need to semantically enrich the mathematical information in scientific papers by associating each mathematical expression with a natural language description. Several applications for accessing mathematical information, such as formula browsing, formula search, and formula disambiguation, utilize descriptions of mathematical expressions. However, these applications utilize different types of textual information to describe expressions. Furthermore, no comparison has been conducted to determine which textual type best describes the expressions. Based on the background described above, this paper provides guidelines for annotating and detecting textual descriptions of mathematical expressions.
Kohlhase, et al. [7] defined the three main challenges in the development of a semantic search for mathematical formulas to be that: (1) mathematical notation is context-dependent, (2) identical mathematical presentations can stand for multiple distinct mathematical objects, and (3) certain variations in notation are widely considered irrelevant. In short, mathematical expressions exhibit a considerable amount of ambiguity. We suggest that search engines for mathematical formulae can tackle these ambiguities by exploiting the extracted descriptions, indexing them as a complement to the abstract mathematical expressions in a formula.
The significance of the descriptions of mathematical expressions in several math-related applications encouraged multiple research projects that aimed to automatically extract descriptions. However, these projects either use small datasets for evaluation [11], implement naive methods [4, 14], or overlook descriptions that include complex phrases [15]. Moreover, each of these projects has a different definition of the term "description". These limitations demonstrate that the description extraction task is not sufficiently well defined. For this reason, we first perform a thorough analysis of the descriptions of mathematical expressions, which requires an annotated corpus containing the relations between expressions and descriptions. The absence of such annotated data made it necessary for us to establish guidelines for annotating descriptions, which were then used to build a corpus.
The two main focuses in the development of mathematical annotation guidelines are: (1) to detect descriptions of mathematical expressions and distinguish them from other mathematical texts, and (2) to define an annotation scheme. Several previous studies [6, 16] have analyzed the linguistics of mathematical discourse. However, these works did not specify any rules or markup to capture and annotate descriptions of mathematical objects. Therefore, we need to define a set of guidelines that is simple enough to implement, yet able to capture all the information related to the descriptions. Subsequently, the gold-standard data used for experiments were constructed based on the annotation dataset produced using these guidelines.
In the description extraction process, the main challenge is to determine the boundaries of the description-candidate text spans. Several previous methods [4, 13, 14] simply take either nouns or domain terms that appear in word windows of predefined length. Another study [15] employed machine learning and used the last compound nouns in the Japanese text as the description candidates. The former approach cannot extract descriptions reliably, as descriptions of mathematical expressions do not necessarily remain in certain word windows. On the other hand, the latter approach struggled to extract descriptions that contain additional phrases or clauses. We address these problems by using a machine learning method and considering the description candidates to be all noun phrases in the same sentence as the target expression.
The contributions of this paper are twofold.
- First, this paper provides guidelines for detecting and annotating descriptions of mathematical expressions. In addition, a corpus containing relationships between mathematical expressions and their descriptions is constructed using these guidelines. The annotation scheme describes the relationships between a description set, full description, and short description, enabling descriptions to be annotated with different degrees of granularity.
- This paper is the first attempt to investigate the potential of several different types of textual information, i.e., fixed context window, apposition, minimal noun phrase, and all noun phrases.
In addition, the proposed framework can be used in other areas of definition annotation, for other types of entities besides mathematical expressions, such as technical terms and chemical formulae.
The remainder of this paper is organized as follows. Section 2 discusses previous work related to this paper. Section 3 describes our description annotation scheme and analysis of the annotation results. Next, Section 4 introduces different techniques for description extraction. In Section 5, we present experimental results for various methods of extracting mathematical descriptions. Finally, our conclusions and ideas for future work are given in Section 6.
2. Related Work
One of the earliest works describing the extraction of textual information on mathematical expressions actually focuses on their disambiguation [4]. Concentrating on mathematical expressions that are syntactically part of a nominal group, this work used the natural language text within which the expressions are embedded to resolve their semantics, thus enabling the disambiguation process. Wolska, et al. [13] complemented the method of [4] by conducting three corpus-based studies on declarations of simple symbols in mathematical writing. This work investigated how many mathematical symbols were explicitly declared in 50 documents. Wolska, et al. [14] then determined that each target mathematical expression has a local and global lexical context. The local context refers to domain terms that occur within the immediately preceding and following linguistic context. The global context is a set of domain terms that occur in the declaration statements of the target expression, or other expressions that are structurally similar to the target expression. These two lexical contexts were then utilized to enhance the disambiguation work.
Nghiem, et al. [11] proposed text matching and pattern matching methods to mine mathematical knowledge from Wikipedia. A Concept-Description-Formula approach was used to mine coreference relations between formulas and the concepts that refer to them. Yokoi, et al. [15] extracted textual descriptions of mathematical expressions from Japanese scientific papers. This work considered only compound nouns as the description candidates.
Subsequently, our previous study [9] on the extraction of descriptions of mathematical expressions showed that machine learning methods outperform left-context and sentence pattern methods. The annotation method in this work considered the description to be the noun phrase containing the most complete information of all the candidates. This procedure results in long text regions, and so this method cannot determine whether each of the extracted descriptions (which appear as short text regions) refers to the same concept as the annotated description. An experimental soft matching setting could not perfectly measure the quality of the extracted description, because it only checked whether the extracted descriptions share some text regions with the annotated descriptions. A more robust annotation guideline was then proposed, introducing full and short descriptions and enabling one description to have a relationship with another [8]. This work improved the annotation guideline proposed in [9], and suggested the importance of reducing each annotated description into other descriptions that appear as shorter text regions but refer to the same concept. These shorter descriptions should be grouped with the former description to give one entity of description. Therefore, it is possible to access different granularities of each annotated description, and better evaluate the extracted descriptions. Following this, we introduced two applications based on the extracted descriptions of mathematical formulas, namely semantic searching and semantic browsing [10].
3. Description Analysis
In the literature on accessing mathematical information, several studies have used textual information associated with mathematical expressions to enrich their semantics [4, 14, 15] In these studies, different types of textual information, such as a fixed-size context window or apposition, were used for enrichment. However, no studies have investigated which type of textual information best describes a mathematical expression. Based on this background, one of the major goals of this paper is to compare commonly used textual types using a corpus with manually annotated mathematical descriptions.
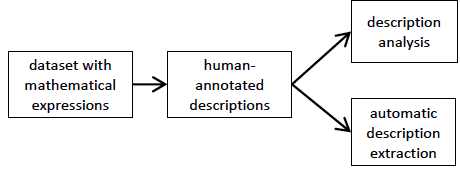
Figure 1: Overview of the procedures in the description extraction task
To analyze the descriptions, we use 40 mathematics papers obtained from the NTCIR (NII Testbeds and Community for Information access Research) Math Understanding Subtask [1]. This set of papers is used as the training data in our experiments. Each mathematical expression in the dataset is replaced with a single unique token, MATH_mathID.
3.1 Annotation Scheme
We assume that a description of a mathematical expression is a textual span that exists in the same sentence as the expression. In addition, descriptions must be distinguished from other forms of mathematical text. Let us consider the pair of sentences "Let G be an n-graph" and "Vertex a is adjacent to vertex b". The text "an n-graph" is a description of G. However, the text "adjacent to vertex b" is not a description, but is a property of a. Thus, the latter text should not be annotated as a description.
In our annotation design, we consider the following properties that apply to many other description extraction tasks:
- Description set. A mathematical expression may have several descriptions. Our annotation scheme enables these multiple descriptions to be annotated as parallel information about the target expression. The term "description set" is used to represent all descriptions of a mathematical expression. The description set contains either zero, one, or multiple descriptions.
- Discontinuous span. A description may appear as several disjoint noun phrases. Our annotation scheme allows several text regions to represent a single description.
- Full and short descriptions. A description can be a nested noun phrase in a parsing tree. From this description, we can derive several new descriptions by removing dependents, e.g., attribute adjectives, noun adjuncts, prepositional phrases, infinitive phrases, or relative clauses. We call these derived descriptions "short descriptions", and the description from which the short descriptions are derived is the "full description". Compared with the full description, short descriptions share the same concept, but are less specific. For example, when a description consists of several discontinuous text regions, each text region that can describe the target expression by itself is annotated as a short description.
Figure 2 depicts an example of the annotation that might be applied to a sentence. Let us consider the annotation of descriptions of the mathematical expression P(zij = t|x,z–ij ). There are two textual descriptions of the expression, so the description set of this expression contains two elements. The first description is composed by two text regions: "the posterior probability" and "of latent topics". A shorter version (short description) of this description can also be annotated, i.e., by annotating the first text region. The second description is "the probability that topic t is assigned to the jth word in the ith paper".
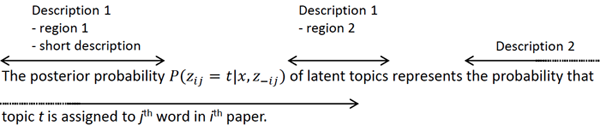
Figure 2: Example of annotations
3.2 Analysis of Annotated Descriptions
The dataset used for description analysis contains 3,644 descriptions. Detailed statistics of this dataset are given in Table 5. The annotation results are used to compare the coverage of the following four types of textual span.
- Fixed context window ("ctx window") [4]. Ten words before and after the target expression are considered as the description.
- Apposition [4, 15]. A preceding noun phrase that has an apposition relation with the target mathematical expression is considered as the description.
- Minimal noun phrase ("minimal NP") [15]. Given a complex noun phrase that contains prepositions, adverbs, or other noun phrases, the "minimal NP" is given by the first compound noun in the phrase.
- All noun phrases ("all NP"). The "all NP" description contains all noun phrases in the target sentence. These noun phrases may range from a simple phrase consisting of only a compound noun to a complex one consisting of a compound noun with a clause, prepositional phrase, wh-adverb phrase, or other phrases.
For a given sentence, we extract the "apposition", "minimal NP", and "all NP" text from the parse tree of the sentence, as produced by the Stanford sentence parser [5]. Note that the analysis results show that the recall from "all NP" is not 100%, which indicates that several descriptions do not appear as noun phrases or cannot be parsed correctly by the parser.
Table 1: Recall potential of four types of textual information
| Matching Type |
Ctx Window |
Apposition |
Minimal NP |
All NP |
| strict |
2.42 |
20.28 |
45.07 |
62.90 |
| soft |
86.56 |
33.20 |
95.05 |
95.22 |
Table 1 summarizes the results. The coverage of each type of textual information is measured in two different matching scenarios, namely strict matching and soft matching. Textual information will pass the strict matching evaluation if its position, in terms of start index and length, is the same as that of a gold-standard description for the same expression. Textual information will pass the soft matching evaluation if its position contains, is contained in, or overlaps with the position of a gold-standard description for the same expression. The soft matching scenario is used to cope with textual information that is not perfectly aligned with the gold-standard description.
The analysis results show that "ctx window" gives good description coverage in the soft matching scenario, but extremely poor coverage under strict matching. Furthermore, "apposition" does not produce a good enough description coverage, even in the soft matching scenario. Therefore, these two types of textual information are not used as description candidates for the machine learning-based extraction method. Conversely, "minimal NP" and "all NP" can capture a moderate number of descriptions in the strict matching scenario, and almost all descriptions under soft matching. Although "minimal NP" and "all NP" only produce approximately 9% higher recall potential than "ctx window" for the soft matching criterion, they achieve much higher recall under strict matching. In addition, the recall potentials of these two types of noun phrases are similar in the soft matching scenario. Therefore, we consider "minimal NP" and "all NP" as description candidates for the machine learning-based extraction method.
4. Extraction Methods
We consider several extraction methods in this paper, namely the nearest noun, sentence pattern, and machine learning-based methods. Unlike the first two methods, machine learning requires a list of description candidates to be constructed for each mathematical expression. This method then determines which of the candidates are correct descriptions for each expression.
4.1 Nearest Noun-Based Method
The nearest noun-based method [4, 15] defines a description as a combination of adjectives and nouns in the text preceding the target mathematical expression. In several cases, a determiner is also included in the combination. This method extracts at most one description, which is composed of a compound noun without additional phrases, for each mathematical expression. For example, let us consider a sentence from Figure 2. The nearest noun method predicts the description of expression e by analyzing the text preceding the expression, i.e., "Additionally, the contraction of an edge". This method detects "an edge" as the description, because this span of text is the nearest noun phrase to the target expression e. The part-of-speech (POS) tags of this detected description are "DT NN".
4.2 Sentence Pattern-Based Method
The sentence pattern-based method [11] naively assumes that the existence of descriptions of mathematical expressions in a sentence can be detected using a certain number of patterns. Whereas previous work [11] implemented an automatic pattern extractor to obtain the sentence patterns, we simplify the process of obtaining these patterns by predefining the six sentence patterns described by Trzeciak [12]. Table 2 lists these six patterns. MATH, DESC, and OTHERMATH represent the target mathematical expression, description of the target expression, and other expressions in the same sentence as the target, respectively.
Table 2: List of sentence patterns
| No. |
Pattern |
| 1 |
. . . (let|set) MATH (denote|denotes|be) DESC . . . |
| 2 |
. . . DESC (is|are) (denoted|defined|given) (as|by) MATH . . . |
| 3 |
. . . MATH (denotes|denote|(stand|stands) for|mean|means) DESC . . . |
| 4 |
. . . MATH (is|are) DESC . . . |
| 5 |
. . . DESC (is|are) MATH . . . |
| 6 |
. . . DESC (OTHERMATH,) * MATH . . . |
4.3 Machine Learning-Based Method
The machine learning-based method formulates description extraction as a binary classification problem by first pairing each mathematical expression with description candidates found in the same sentence as the expression. It is assumed that a description is a noun phrase. Thus, description candidates can be obtained by extracting noun phrases from the parse tree of the sentence containing the target expression. Moreover, because "all NP"and "minimal NP" [15] delivered the highest recall potential in the description analysis process (see Table 1), these two types of noun phrases are considered as description candidates for the machine learning-based method. Once each mathematical expression has been paired with all noun phrases in the same sentence that match the selection criteria, features are extracted for each pair. The machine learning-based method relies on the sentence patterns, POS tags, parse trees, and dependency trees produced by the Stanford sentence parser [3, 5].
Next, the expression—noun phrase pairs are run through a binary classifier to determine whether the noun phrase is a description for the expression. Table 3 gives the features extracted for each pair used in the classification. Features 1—6 are obtained by applying the six sentence patterns listed in Table 2. Features 7—17 are produced by examining the surface text and POS tags of the sentence containing the particular expression—description pair. Finally, features 18—23 are generated from the shortest path between target expression and paired description candidate in the dependency tree.
Table 3: List of machine learning features
| No. |
Feature |
| 1-6 |
Sentence patterns in Table 2 |
| 7 |
If there is a colon between the desc candidate and the paired expr |
| 8 |
If there is a comma between the desc candidate and the paired expr |
| 9 |
If there is another math expr between the desc candidate and the paired expr |
| 10 |
If the desc candidate is inside parentheses and the paired expr is outside parentheses |
| 11 |
Word-distance between the desc candidate and the paired expr |
| 12 |
Position of the desc candidate relative to the paired expr (after or before) |
| 13 |
Surface text and POS tag of two preceding and following tokens around the desc candidate |
| 14 |
Surface text and POS tag of the first and last tokens of the desc candidate |
| 15 |
Surface text and POS tag of three preceding and following tokens around the paired math expr |
| 16 |
Unigram, bigram, and trigram of features 15 and 13 that is combined with feature 14 |
| 17 |
Surface text of the first verb that appears between the desc candidate and the target math expr |
| 18 |
Hop-distance (in the dependency tree) between the desc candidate and the paired math expr |
| 19 |
Dependencies with length of 3 hops, that is from an undirected path connecting desc candidate with paired math expr and starts from the desc candidate |
| 20 |
Direction of feature 19 with respect to the candidate (incoming or outgoing) |
| 21 |
Dependencies with length of 3 hops, that is from an undirected path connecting desc candidate with paired math expr and starts from the paired expr |
| 22 |
Direction of feature 21 with respect to the expression (incoming or outgoing) |
| 23 |
Unigram, bigram, and trigram of features 19 and 21 |
5. Description Extraction Experiments
We conducted description extraction experiments on 50 mathematics papers obtained from the NTCIR Math Understanding Subtask [1]. Table 4 displays the inter-annotator agreement scores measured on this dataset.
Table 4: Inter-annotator agreement
| |
F1-Score |
Kappa |
Alpha |
| full descriptions |
strict: 86.70
soft: 97.01 |
89.93 |
76.30 |
| full and short descriptions |
strict: 90.14
soft: 96.83 |
N/A |
N/A |
The annotated dataset provides complete knowledge about descriptions of each mathematical expression, i.e., full descriptions and short descriptions. During the investigation, several full descriptions were found to appear as discontinuous text regions. In the experiments, we simplified this circumstance by only extracting full descriptions that appear as single continuous text regions. Thus, both full and short descriptions could be extracted using the same methods.
Three metrics were used to measure the performance of the automatic description extraction process: precision, recall, and F1-score. However, in the case of short description extraction, a slightly different counting method was used. Instead of the number of matching short descriptions, we counted the number of full descriptions that shrink into the matching short descriptions.
5.1 Experimental Setup
Three automatic description extraction methods were applied to the annotation results: nearest noun [4, 15] (baseline), sentence pattern [11], and machine learning. In addition, we also examined the performance of four types of textual information as the description candidates: "ctx window", "apposition", "minimal NP", and "all NP". In this experiment, 40 papers formed the training set, and the remaining 10 were used as the test set. The statistics of these sets are summarized in Tables 5 and 6. The descriptions are assumed to be noun phrases, although these statistics show that not every description can be detected as a noun phrase. Thus, the actual number of descriptions used by the machine learning method to train the model is less than the initial number.
Table 5: Dataset statistics
| |
Training Set |
Testing Set |
Total |
| #math (distinct / all) |
5,456 / 10,948 |
1,123 / 2,386 |
6,579 / 13,334 |
| #math having desc (distinct / all) |
2,220 / 3,499 |
521 / 824 |
2,741 / 4,323 |
| #math having full desc as NP (distinct / all) |
1,681 / 2,541 |
333 / 493 |
2,069 / 3,124 |
| #math having short desc as NP (distinct / all) |
1,705 / 2,599 |
392 / 598 |
2,097 / 3,197 |
| #full desc |
3,644 |
874 |
4,518 |
| #full desc as NP |
2,298 |
513 |
2,811 |
| #full desc as minimal NP |
1,640 |
377 |
2,017 |
| #short desc |
3,824 |
919 |
4,743 |
| #short desc as NP |
2,725 |
630 |
3,355 |
| #short desc as minimal NP |
2,600 |
603 |
3,203 |
Table 6: Instances statistics
| |
Full Descriptions |
Short Descriptions |
| #pos |
#neg |
#pos |
#neg |
| "any noun phrase" as description candidate |
| training set |
2,298 |
92,688 |
2,725 |
92,261 |
| testing set |
515 |
23,332 |
630 |
23,217 |
| "minimal noun phrase" as description candidate |
| training set |
1,640 |
70,500 |
2,600 |
69,540 |
| testing set |
377 |
17,419 |
603 |
17,193 |
Having extracted the features, we trained a machine learning model using an SVM algorithm. The training process was performed using LibSVM [2] with a linear kernel and a default regularization parameter value of C = 1.0. Finally, this model was used to predict descriptions in the test step. Five types of SVM model were built for the experiment, each employing a different set of features. Type 1 applies basic features and uses "all NP" (features 7—17), type 2 applies basic and sentence pattern features and uses "all NP" (features 1—17), type 3 applies basic and dependency features and uses "all NP" (features 7—23), type 4 applies all features and uses "all NP" (features 1—23), and type 5 applies all features and uses "minimal NP" (features 1—23).
5.2 Experimental Results and Discussion
Table 7 presents the precision, recall, and F1-scores obtained by the classifiers. This table shows that, of the four types of textual information, "apposition" gives the highest F1-score, but "minimal NP" and "all NP" produce the highest recall. The SVM models should increase the precision of the detected descriptions that appear as noun phrases. Although these precision improvements can decrease the recall performance, they tend to enhance the overall metric of the F1-score. These improved F1-scores indicate that the SVM models are effective.
Table 7: Experimental Results
| Methods |
Strict Matching |
Soft Matching |
| P |
R |
F1 |
P |
R |
F1 |
| Full Description |
| ctx window |
0.36 |
1.72 |
0.59 |
16.65 |
80.66 |
27.60 |
| apposition |
35.31 |
21.17 |
26.47 |
55.53 |
33.30 |
41.63 |
| minimal NP |
2.12 |
43.14 |
4.04 |
6.93 |
93.71 |
12.91 |
| all NP |
2.16 |
58.70 |
4.17 |
7.88 |
94.28 |
14.55 |
| nearest noun |
27.40 |
22.20 |
24.53 |
46.33 |
37.53 |
41.47 |
| sentence ptn |
19.80 |
26.66 |
22.72 |
46.39 |
62.59 |
53.28 |
| ML_basic |
69.03 |
35.70 |
47.06 |
91.15 |
41.65 |
57.17 |
| ML_basic_ptn |
76.28 |
40.85 |
53.20 |
90.60 |
46.57 |
61.52 |
| ML_basic_dep |
68.20 |
35.58 |
46.77 |
92.11 |
41.76 |
57.47 |
| ML_all_allNP |
75.05 |
40.96 |
53.00 |
90.34 |
47.48 |
62.25 |
| ML_all_minNP |
79.37 |
31.69 |
45.30 |
89.68 |
35.70 |
51.07 |
| Short Description |
| ctzx window |
0.33 |
1.60 |
0.55 |
16.60 |
80.32 |
27.51 |
| apposition |
40.65 |
24.37 |
30.47 |
55.15 |
33.07 |
41.34 |
| minimal NP |
3.23 |
65.68 |
6.15 |
4.91 |
93.25 |
5.77 |
| all NP |
2.50 |
67.85 |
4.81 |
5.77 |
94.16 |
10.87 |
| nearest noun |
32.20 |
26.09 |
28.82 |
46.19 |
37.41 |
41.34 |
| sentence ptn |
17.84 |
24.03 |
20.48 |
46.22 |
62.36 |
53.09 |
| ML_basic |
68.83 |
42.22 |
52.34 |
91.65 |
46.91 |
62.06 |
| ML_basic_ptn |
78.70 |
49.66 |
60.89 |
89.53 |
53.66 |
67.10 |
| ML_baisc_dep |
69.67 |
43.25 |
53.37 |
91.54 |
49.08 |
63.90 |
| ML_all_allNP |
77.70 |
50.11 |
60.93 |
90.09 |
55.26 |
68.50 |
| ML_all_minNP |
84.25 |
52.63 |
64.79 |
91.76 |
57.32 |
70.56 |
The experimental results show that all five SVM models outperform the baseline and sentence pattern method. The SVM models that use only basic and dependency graph features already outperform the baseline methods, except for the recall of the sentence pattern method under soft matching. Moreover, it can be seen that the fourth and fifth SVM models, which both implement all features, give the best performance. Furthermore, the results indicate that sentence pattern-based features have a significant positive influence on the performance of the SVM models. This disproves a previous finding that sentence pattern features do not influence the extraction performance [15]. Considering the statistics of the extraction results, shown in Table 7, we note that the SVM models give good precision performance, i.e., up to 92%, and moderate recall performance, i.e., up to 57%.
For full description extraction, the SVM models using "all NP" achieve the highest F1-scores. Among these SVM models, that which applies all features attained the best performance. This model delivered the highest recall for both strict and soft matching, and gave the highest F1-score under soft matching.
The recall of full descriptions using "all NP" is better than that using "minimal NP", because full descriptions tend to be longer and to appear as a complex noun phrase. This type of phrase can be detected by the "all NP" approach, but not by "minimal NP". Therefore, the recall potential of "minimal NP" is not as high as that of "all NP", and this massively affects the recall and F1-score performance in the full description extraction.
For short description extraction, of the models that use the "all NP" approach, the SVM model that applies all features gave the best F1-score. The results of short description extraction indicate that extracting short descriptions using "minimal NP" gives better results than using "all NP". This is because of the textual complexity (in the parse tree) of the description, and the ratio of the number of positive instances to the total number of instances. Short descriptions have a shorter text length than full descriptions, and in most cases they appear as a single compound noun without any additional clauses or phrases. Therefore, both "all NP" and "minimal NP" approaches are capable of detecting short descriptions. Opting for "all NP" instead of "minimal NP" as the description candidate selection criterion will increase the number of instances in the training data. Thus, the ratio of positive instances to the total number of instances in the "all NP" approach is smaller (more imbalanced) than that using "minimal NP". This imbalance makes the SVM models trained using "minimal NP" perform better than those trained using "all NP"as the description candidate criterion.
The straightforward sentence pattern method gives quite good recall in soft matching scenarios. However, the descriptions extracted using this method are not quite the same as the gold-standard data, as shown by the fact that the recall performance of this method decreases once strict matching is applied. Moreover, its precision in both matching scenarios is also much lower than that obtained by the machine learning-based method.
Figures 3 and 4 show the correlation between the number of training instances and the overall F1-score performance for full and short description extraction, respectively. These two figures clearly show that larger sets of training data lead to better results. Figure 3 indicates that the F1-score of the SVM models that use all features and either "all NP" or "minimal NP" become stable once 80% of the training data is employed. Moreover, these two models require only 10% and 20% of the training data, respectively, to outperform the baseline method. Figure 4 shows that "all NP" and "minimal NP" models perform steadily after they are trained using at least 70% of the training data. In addition, both models are capable of outperforming the baseline method using only 10% of the training data. Another detail that presents itself in these two figures is that the difference between the F1-scores of models that use "all NP" and "minimal NP" for full description extraction is larger than that for short description extraction. For full description extraction, once the performance of both models has stabilized, the F1-score differences are 7.29% — 8.00% and 10.62% — 11.52% for the strict and soft matching scenarios, respectively. For short description extraction, however, the differences are only 2.76% — 4.36% and 1.71% — 3.56%. These F1-score differences imply that the SVM model that uses "all NP"and all features is preferable to the "minimal NP"model with respect to the number of extracted descriptions.
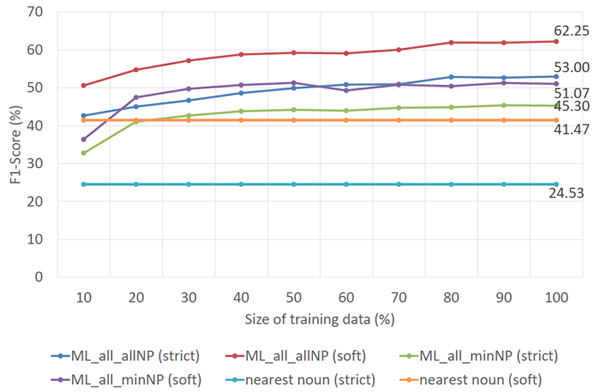
Figure 3: Extraction performance of full descriptions with respect to the size of training data.
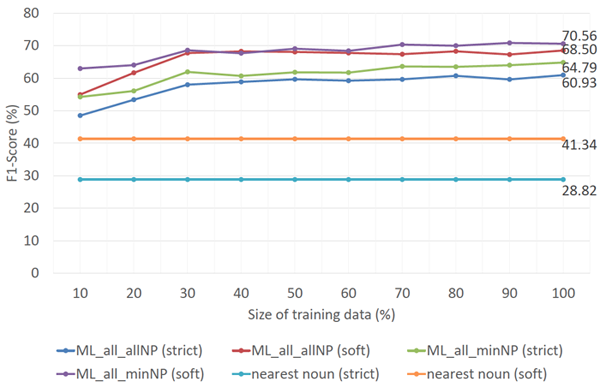
Figure 4: Extraction performance of short descriptions with respect to the size of training data.
5.3 Analysis of Extraction Results
Table 8 presents some examples of full description extraction using the third SVM model. The first three examples show correct descriptions extracted by the model. These descriptions pass both the strict and soft matching evaluation. However, several description extraction results that pass the soft matching criterion do not achieve a strict matching. One of the reasons most frequently encountered is that the noun phrases obtained from the sentence parser do not line up perfectly with the descriptions. The fourth example illustrates this problem. The noun phrase obtained from the sentence parser includes the word "so"; consequently, the extracted description contains this word. Another reason is that the SVM model only extracts those descriptions that appear as single continuous text regions. Therefore, descriptions that appear in two or more parts are not extracted. This is illustrated in the fifth example. Although full descriptions cannot be extracted, the model manages to extract the first text region of the description. This result does not pass the strict matching, yet passes the soft matching evaluation.
Table 8: Output example and error analysis
| Math Exp |
Sentences and Full Descriptions |
Remark |
| MATH_102 |
... the number of permutations of length MATH_100 with exactly one occurrence of MATH_101 is MATH_102.
Gold: the number of permutations of length MATH_100 with exactly one occurrence of MATH_101
System: same as the gold-standard one |
Correct |
| MATH_127 |
Here, MATH_127 is the MATH_128-bracket defined by MATH_129.
Gold: the MATH_128-bracket defined by MATH_129
System: the MATH_128-bracket AND the MATH_128-bracket defined by MATH_129 |
Correct |
| MATH_234 |
Let MATH_234 be the EGF for the number of permutations that avoid MATH_235.
Gold: the EGF for the number of permutations that avoid MATH_235
System: same as the gold-standard one |
Correct |
| MATH_35 |
... so the complement of MATH_34 is MATH_35.
Gold: the complement of MATH_34
System: so the complement of MATH_34 |
Correct in soft matching, but not in strict matching. |
| MATH_47 |
... the complexes MATH_97 for primitive MATH_48 are all isomorphic.
Gold: the complexes for primitive MATH_48
System: the complexes |
Correct in soft matching, but not in strict matching. |
| MATH_72 |
... since the only permutation with no descent and no inversion is the increasing permutation MATH_72.
Gold: the only permutation with no descent and no inversion
System: N/A |
Unsuccessful extraction. |
| MATH_209 |
Kitaev, in [45], introduced a further generalization of generalized patterns (GPs),
namely the partially ordered generalized patterns or POGPs. ...An example of such pattern is MATH_209, ...
Gold: the partially ordered generalized patterns or POGPs
System: N/A |
Unsuccessful extraction. |
The description of MATH_72, i.e., "the only permutation with no descent and no inversion", in the sixth example has not been extracted successfully. This description, in fact, has a similar pattern to the first example, i.e., "description definitor target_expression". The only difference is that MATH_72 is part of a nominal group and is immediately preceded by a noun phrase, whereas MATH_102 is not immediately preceded by a noun phrase. Further analysis shows that the SVM model has difficulty extracting descriptions following the pattern "description definitor NP (target_expression)" when the target expression is part of a nominal group and has an immediately preceding noun phrase. The seventh example shows another type of description that cannot be extracted. This case occurs because of the simplification to the experiments, i.e., the assumption that descriptions appear in the same sentence as the target mathematical expressions. Therefore, the model overlooks descriptions within a different sentence to the target expression.
Having analyzed these examples of false instances, some additional methods to improve our proposed description extractor system can be suggested. The first possible method is to automatically implement a sentence pattern extractor, and then use the extracted patterns to either enrich the machine learning features, or to directly extract descriptions that cannot be detected by the machine learning method. This might help extract the description in the sixth example. This method can be leveraged as follows to solve the problem found in the fifth example, extracting descriptions that appear in separated text regions. After obtaining the pattern of discontinuous descriptions, this method extracts the related text regions. Further analysis can then be conducted to check whether the concatenation of these regions can be parsed as a noun phrase. If so, it becomes a description candidate; if not, it is strongly assumed not to be a description.
The fourth example illustrates the dependency of the current method on the sentence parser. We encountered several cases where the parser gave the wrong parse tree structures for the descriptions. This is caused by the parser giving the wrong POS tag for a word within a description; specifically, the nouns pixel, values, and tag are sometimes tagged as verbs. Using a parser that is better suited to parsing sentences containing mathematical expressions may improve the precision of detecting noun phrases. The seventh example requires coreference resolution to find descriptions referring to the same mathematical expressions.
6. Conclusion
This paper has discussed methods of detecting, annotating, and extracting descriptions of mathematical expressions. The annotation guidelines given here introduce relationships among a description set, full description, and short description, enabling descriptions to be annotated with different degrees of granularity. Subsequently, the description analysis conducted on the annotated dataset indicated that the "all NP" approach returns a higher recall potential than other types of textual information. We proposed three methods for automatic description extraction: nearest noun (baseline), sentence pattern, and machine learning (SVM). The results of description extraction indicated that the machine learning model using the "all NP" approach and all possible features is better for detecting full descriptions than models that use "minimal NP". This is because full descriptions tend to appear as complex noun phrases, which can be detected by the "all NP" approach, but not by "minimal NP". The results also showed that sentence pattern-based features had a significant positive influence on the performance of the SVM models. Additionally, the sentence pattern method, as a straightforward approach, performs quite well in terms of the recall under the soft matching scenario. However, its extraction results are not precise, and hence the performance level drops under strict matching.
In future research, we will incorporate several improvements. For example, we intend to implement an automatic sentence pattern extractor, and then use the patterns obtained to extract descriptions that cannot be detected by machine learning methods. This will enable the extraction of descriptions with separated text regions. We will also apply coreference resolution to extract descriptions that are in different sentences to the target mathematical expression. Furthermore, we plan to investigate the degree to which the interlinking of mathematical expressions represents the interlinking of papers. Our proposed framework could also be applied to entities other than mathematical expressions, such as chemical formulas or genes.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 2430062, 25245084, and 14J09896.
References
[1] A. Aizawa, M. Kohlhase, and I. Ounis. Ntcir-10 math pilot task overview. In Proc. of the 10th NTCIR Conference, 2013.
[2] C.-C. Chang and C.-J. Lin. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2:1—27, 2011. http://doi.org/10.1145/1961189.1961199
[3] M.-C. de Marneffe, B. MacCartney, and C. Manning. Generating typed dependency parses from phrase structure parses. In Proc. of LREC-06, 2006.
[4] M. Grigore, M. Wolska, and M. Kohlhase. Towards context-based disambiguation of mathematical expressions. In Proc. of the Joint conference of ASCM-09 and MACIS-09, 2009.
[5] D. Klein and C. Manning. Accurate unlexicalized parsing. In Proc. of the ACL-03, pages 423—430, 2003. http://dx.doi.org/10.3115/1075096.1075150
[6] M. Kohlhase. An Open Markup Format for Mathematical Documents OMDOC [Version 1.2]. LNAI. Springer Verlag, 2009.
[7] M. Kohlhase and I. A. Sucan. A search engine for mathematical formulae. In Proc. of AISC, number 4120 in LNAI, pages 241—253. Springer Verlag, 2006. http://dx.doi.org/10.1007/11856290_21
[8] G. Kristianto, M.-Q. Nghiem, N. Inui, G. Topić, and A. Aizawa. Annotating mathematical expression definitions for automatic detection. In
Proc. of the CICM Workshop MIR-12, 2012.
[9] G. Kristianto, M.-Q. Ngiem, Y. Matsubayashi, and A. Aizawa. Extracting definitions of mathematical expressions in scientific papers. In Proc. of the 26th Annual Conference of JSAI, 2012.
[10] G. Kristianto, G. Topić, M.-Q. Nghiem, and A. Aizawa. Annotating scientific papers for mathematical formulae search. In Proc. of the 5th ESAIR of The 21st ACM CIKM, pages 17—18, 2012. http://doi.acm.org/10.1145/2390148.2390158
[11] M.-Q. Nghiem, K. Yokoi, Y. Matsubayashi, and A. Aizawa. Mining coreference relations between formulas and text using wikipedia. In Proc. of the 2nd NLPIX, pages 69—74, 2010.
[12] J. Trzeciak. Writing Mathematical Papers in English: A Practical Guide. EMS, 1995. http://dx.doi.org/10.4171/014
[13] M. Wolska and M. Grigore. Symbol declarations in mathemaical writing: A corpus study. In Proc. of the CICM Workshop DML-10, pages 119—127, 2010. ISBN 978-80-210-5242-0.
[14] M. Wolska, M. Grigore, and M. Kohlhase. Using discourse context to interpret object-denoting mathematical expressions. In Proc. of the CICM Workshop DML-11, pages 85—101, 2011. ISBN 978-80-210-5542-1. URL
http://www.dml.cz/dmlcz/702605
[15] K. Yokoi, M.-Q. Nghiem, Y. Matsubayashi, and A. Aizawa. Contextual analysis of mathematical expressions for advanced mathematical search. In Proc. of the 12th CICLing, 2011.
[16] C. Zinn. Understanding Informal Mathematical Discourse. PhD thesis, Universitat Erlangen-Nürnberg Institut für Informatik, 2004.
About the Authors
 |
Giovanni Yoko Kristianto is a PhD student in the Graduate School of Information Science and Technology at The University of Tokyo. He received his bachelor's and master's degrees from Gadjah Mada University and The University of Tokyo, respectively. His research interests include machine learning, information retrieval, knowledge and information extraction, and link prediction.
|
 |
Goran Topić has received a master's degree from the Graduate School of Interdisciplinary Information Studies at the University of Tokyo.
|
 |
Akiko Aizawa is a professor in Digital Content and Media Sciences Research Division at National Institute of Informatics. She is also an adjunct professor at the Graduate School of Information Science and Technology at the University of Tokyo. Her research interests include statistical text processing, linguistic resources construction, and corpus-based knowledge acquisition.
|
|